Geometria Espacial
Relação de Euler
Em todo poliedro convexo é válida a relação seguinte:
V - A + F = 2
em que V é o número de vértices, A é o número de arestas e F, o número de faces.
Observe os exemplos:
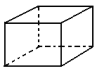
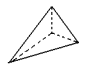
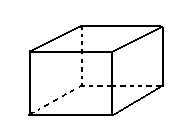
V=8 A=12 F=6
8 - 12 + 6 = 2
| 
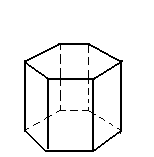
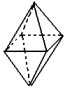
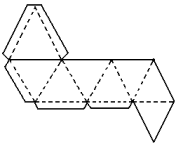
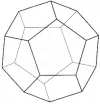
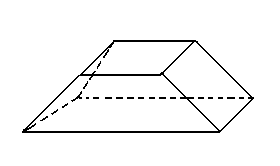
V = 12 A = 18 F = 8
12 - 18 + 8 = 2
|
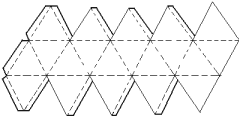
Poliedros platônicos
Diz-se que um poliedro é platônico se, e somente se:
a) for convexo;
b) em todo vértice concorrer o mesmo número de arestas;
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler.
Assim, nas figuras acima, o primeiro poliedro é platônico e o segundo, não-platônico.
Prismas
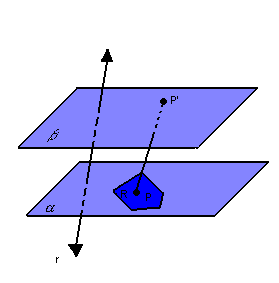
Na figura abaixo, temos dois planos paralelos e distintos,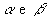 
, um polígono convexo R contido em 
e uma reta r que intercepta , mas não R:
, um polígono convexo R contido em e uma reta r que intercepta 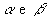, mas não R:
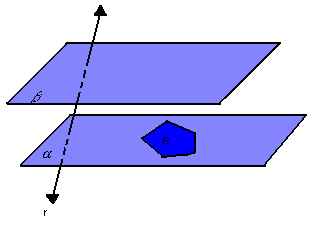
Para cada ponto P da região R, vamos considerar o segmento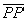 
, paralelo à reta r 
:
, paralelo à reta r :
Assim, temos:
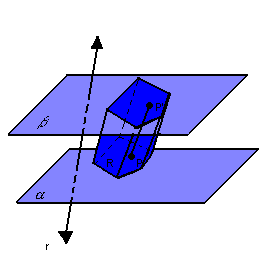
Chamamos de prisma ou prisma limitado o conjunto de todos os segmentos congruentes paralelos a r.
paralelos a r.
semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em que o plano de cada um deixa as outras semi-retas em um mesmo semi-espaço. A figura formada por esses ângulos é o ângulo poliédrico.
